1.2 Symbols and Expressions

We now start a systematic definition of Refal. A summary of the language's syntax is also appended as Reference Section B.

A symbol in Refal is the minimal syntactic element of data structures. We use the following kinds of symbols:

• characters,
• compound symbols , in particular, identifiers ( also known as symbolic names),
• whole non-negative numbers (macrodigits)

Characters are enclosed in single quotes, e.g. 'a', or '+'. A string of characters is enclosed in quotes as a whole. Thus 'a+b' is a sequence of three symbols: 'a', '+', and 'b'. The sequence must not be broken by line transfers. A string may consist of zero characters: ''; it is an empty expression -- just nothing; it is not a symbol.

To represent a quote inside a string, we put the special escape character \ in front of it: \' . Thus '*,\'' is a string of three symbols: an asterisk, a comma, a single quote.

A compound symbol is a sequence of characters enclosed in double quotes, e.g. "a+b" . A compound symbol makes exactly one symbol, even if there are no characters in it: "". A double quote inside a compound symbol must be used with an escape: \". Thus "_a\"pig\"" is a compound symbol formed from the following characters: underlining, 'a', space, double quote, 'p', 'i', 'g', double quote. A single quote within a compound symbol may be used both with and without an escape. The general rule about the use of quotes in strings and compound symbols is: a quote in a sequence of characters embraced by the same quotes must be used with escape; if the embracing quotes are of the other kind, the quote can be used both with, and without the escape. The escape \ itself (backslash) is always represented as \\ .

There are several characters of a special importance for Refal that can be used in strings both in their "natural form", and preceded by escape \; they are: ( , ) , < , > . Thus, \< is the same as just <.

Besides the usual printable characters, there are special characters formed using the escape:

\n new line

\r carriage return

\t horizontal tab

One more use of the escape is to treat every byte as a symbol; the character \xHH, where each H is a hexadecimal digit, stands for a byte with the code HH.

An identifier is a compound symbol which starts with a letter and consists of letters, digits, hyphens - and underlinings _. In such a compound symbol the embracing double quotes may be, and usually are, dropped.

As in other compound symbols, the case of letters in identifiers matters: "function" is not the same as "Function".

Examples of valid identifiers:

 "x1"    x1    x-y    Y5t66    catch-22     Hit-and-run     "the_last_stage"

 "1x"      1x      x+y     "input/output"     "\s5"     'Y5t66'

 '\s5'      "\s5"

Macrodigits in our implementation of Refal-5 are integers in the range from 0 to 2³²-1. Greater numbers can be composed from macrodigits using the base 2³² , as decimal numbers are composed from the ordinary (decimal) digits; this explains the name. To represent negative whole numbers we put '-' in front of digits, as we do when using decimal digits. Like letter-characters, which are different from letter-identifiers, digit-characters are different from number-symbols. '1' is not the same as 1 . While the former is an ordinary decimal digit, the latter is a macrodigit.

Examples: 3306 is one symbol -- a macrodigit with the numerical value of 3306 . '-'25 is a sequence of two symbols; the character '-' followed by the macrodigit 25 . Together they will be taken by arithmetic functions as the number -25. The following:

2543 88918 9

2543*2⁶⁴ + 88918*2³² + 9

NOTE: If you write something like '--'25 this will not be a syntax error. This is a quite legitimate string of three symbols. An error will ensue if you try to use it as an operand in an arithmetic function.

Conspicuous here is the absence of real numbers. In the advanced versions of Refal, (Refal-6 and Refal+), we have Refal symbols which represent real numbers. But in Refal-5 we stick to the principle that Refal is dealing with precisely defined symbols and leaves no details of representation and handling for some computer to decide. To work with real numbers, the user must invent his own representation of real numbers through natural (whole non-negative) numbers, for example as terms of the form:

  (Real SN (M) SCH (CH) )

  SN M (2^32)^(SCH CH)

It remains to define operations on such real numbers. They will not be as fast as when real numbers are represented by computer words, but we do not expect Refal doing much work with real numbers.

Generally, blanks are not counted as symbols; blanks and line transfers are used to separate lexical units of Refal whenever necessary and to position them nicely on the page. The only situation where a blank becomes a symbol is when it is used inside quotes. While "" is a compound symbol with a blank-name , '' is a blank-character. When used between quoted strings, a blank tells us to unquote them separately. Thus 'a''b' is a string of two characters, a and b , while 'a\'b' is a string of three characters: a , the quote, and b .

To create data structures in Refal we use parentheses. Unquoted parentheses are not symbols but special signs of Refal. We also refer to them as structure brackets in order to distinguish them from the angular evaluation brackets. Structure brackets must be properly paired according to the well-known simple rules. We call any sequence of symbols and parentheses whose parentheses are correctly paired an object expression. More precisely, an object expression is a sequence of a finite number of terms, where a term is either a single symbol or an expression enclosed in parentheses. The number of terms in an expression may be zero so that an empty object (just nothing) is a legitimate expression. Here are other examples of expressions:

  A
  (A'+'B)'*'(C'-'D)
  Begin (Ho-ho-ho '(' ('A joke')) End
  ()
  (()'100'100() (()) ) [[

  ) End
  A ( B)((C)
  ( A ')';

  (A'+'B)'*'(C'-'D)

  (A + B) * (C - D)

In algebra we use expressions to represent certain sequences of operations over numbers and variables; parentheses in expressions indicate the order in which to perform operations. If the expression above is understood as an algebraic expression, it would be represented by the tree structure shown in Fig. 1.1.

Figure 1.1 The tree for the algebraic expression:

It should be stressed that the concept of expression in Refal is more general. We do not assume any special interpretation of expressions; they can be used in various ways. A Refal expression is simply a structured object built in a certain way from symbols and structure brackets. For each structure bracket there is exactly one paired bracket of the opposite kind. Together they form a sort of box or pouch. They delimit a sub-system of the overall system, which is a part of the whole, but which still preserves its unity. If you locate one boundary of this sub-structure, the other boundary is uniquely defined. The relation between a system and its sub-systems is a very important aspect of the world. When we create symbolic models of the world, structure brackets model this relation. If the piano, violin, and viola are in Ann's apartment, while the cello and bass are in Bob's, this situation can be modeled by the Refal expression:

  Ann-apt(Piano Violin Viola) Bob-apt(Cello Bass)

A Refal expression can be represented by a tree, like an algebraic expression. However, if we treat an expression as just a Refal expression, without interpreting it in any way, the tree should be somewhat different. In Fig. 1.1 we raised the operations over their arguments. But if we do not interpret the expression, then A + B is just a concatenation of three symbols, and they all should be on the same level. The tree should look as in Fig. 1.2. The leaves (end-nodes) of the tree are symbols; the other nodes are parenthesized subexpressions.

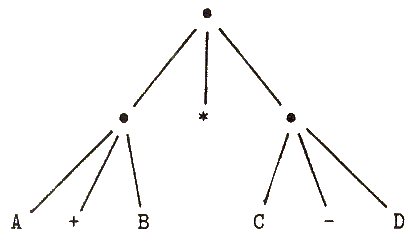
Figure 1.2 The tree for the Refal expression

Another use of the second dimension in picturing expressions is to connect the paired parentheses by lines, as if by strings; the hierarchy of subexpressions is then made more visible (see Fig. 1.3). When Refal expressions are represented in a computer, the address of the paired parenthesis is stored with each parenthesis, so that it becomes possible to jump from a parenthesis to its complement in one step, as if running along these strings.

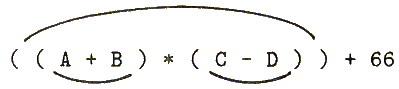
Figure 1.3 Paired parentheses are connected for clarity.

Exercise 1.1 Write the string Joe's Pizza is "cute" as a string of characters and a compound symbol.

Exercise 1.2 Write -2³⁶ as a whole number in Refal.