3.3 Implicit and Explicit Recursion

Recall function Blanks defined in Sec. 3.1. Now we want to modify it so that only those repeated blanks which are not inside quotes are eliminated -- a common situation with programming languages. Then we cannot use the pattern e1''e2 with an open e-variable, but must examine symbols one by one. First of all, let us redefine the old function Blanks in this fashion:

  Blanks {
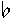
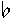     ''e.1 = <Blanks '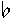'e.1>; 
     s.A e.1 = s.A <Blanks e.1>;
  * End of job 
     = ; };

  Blanks {
  *1.Delete one of two adjacent blanks 
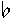
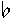     ''e.1 = <Blanks '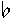'e.1>;   
  *2.If a quote, jump to the next quote
     '\''e.1'\'' e.2 = '\''e.1'\'' <Blanks e.2>;  
  *3.No pair for a quote: an error
     '\'' e.1 = 
       <Prout 'ERROR: no pair for quote in 'e.1>;
  *4.Regular symbol
     s.A e.1 = s.A <Blanks e.1>;
  *5.End of job
     = ; };

Whenever open variables can be used in an algorithm, they should be used for the sake of efficiency. Even though an algorithm with an open variable may be essentially the same as in the case of symbol-by-symbol processing, the number of steps of the Refal machine can be much less. Because of the overhead in the implementation of a step, the program with an open variable will work faster. In the last definition of Blanks we left an open variable, namely e.1 , in sentence 2 in order to jump directly to the closing quote.

It should be remembered, however, that when there are more open variables than one, the universal matching algorithm, as described in Chapter 2 , may not be the most efficient solution to the problem.

Consider this sentence:

  <Sub-a-z e.1 'a'e.X'z' e.2> = (e.1) 'a'e.X'z' (e.2)

It locates a substring which starts with 'a' and ends with 'z' . If the argument actually contains such a substring, the algorithm will work quite efficiently. The first entry of 'a' will be discovered and then so will be the first entry of 'z' after it. But suppose that the argument contains no 'z s, but there are a lot of 'a s, for instance:

  'abababababababababababababababababababaababab' 

To eliminate this inefficiency, we have to break the process into two functions, like this:

  Sub-a-z {
     e.1'a'e.2 = <Find-z (e.1'a')e.2>;
  /* Find 'a' and pass the argument to Find-z */
     e.2 = <Prout 'No substring a-z'>; }
   
  Find-z {
     (e.1'a') e.X'z'e.2 = (e.1) 'a'e.1'z' (e.2);
     (e.1) e.2 = <Prout 'No substring a-z'>; 
         }

Generally, it is always safe to disguise a linear scan as a matching process with one open variable. The case of several open variables requires, if you are concerned with efficiency, a special examination in each case. Redefinition to eliminate possible inefficiencies, like in the example above, is usually fairly easy.

Open and repeated e-variables, as well as repeated t-variables, allow us to hide recursion behind a pattern. If for some reason we want all loops of recursion to be explicit (and we do want this when working on function transformation), we can rewrite every definition so that it does not use variables of those types. For instance, the function Sub-a-z does not look recursive: it either calls Find-z (which never calls Sub-a-z back), or the built-in function Prout . But it is actually recursive because of the open variable in the first sentence. It can be redefined as follows:

  Sub-a-z {
     e.1 = <Sub-a-z-1 ()e.1>; }
   
  Sub-a-z-1 {
  *1.'a' is found. Control is passed to Find-z. 
     (e.1) 'a'e.2 = <Find-z (e.1'a') e.2>;
  *2.Recursion: jump over any symbol distinct 
  *   from 'a'. 
     (e.1) s.X e.2 = <Find-a-z-1 (e.1 s.X) e.2>;
  *3.The string is exhausted without finding 'a'
     (e.1) = <Prout 'No substring a-z'>; }

One might notice that we used a certain system in rewriting the definition of this function. It is to enclose open e-variables in parentheses and introduce auxiliary functions which simulate the lengthening of open variables. This process of eliminating implicit recursion can be easily implemented in a program and performed automatically.

Exercise 3.3 The function of equality between arbitrary expressions (not necessarily strings) can be defined as follows:

  Equal {
     (e.1)(e.1) = T;
     (e.1)(e.2) = F; }

  F {
     e.1 s.X e.2 s.X e.3 = s.X e.2 s.X;
     e.1  = <Prout 'No repeated symbols'>; }