3.7 Dealing with Nested Parentheses

Refal takes parentheses very seriously. Under no circumstances can we treat them as symbols (this does not apply, of course, to characters '(' and ')' , which are as good as other symbols). An expression represents a tree where symbols are leaves, and parenthesized terms are subtrees. If we want, for example, to change '+' into '-' throughout all levels of parentheses, we can do that only by explicitly defining the process of entering parentheses. The simplest solution is:

  * Change every '+' to '-', depth-first order.
  Chpm {
     '+'e.1 = '-'<Chpm e.1>;
     s.X e.1 = s.X <Chpm e.1>;
     (e.1)e.2 = (<Chpm e.1>) <Chpm e.2>;
      = ;  }

This way of processing trees is known as the depth-first method. Whenever we meet a subtree, i.e., come to a left parentheses, we first go down (inside), as the first call of Chpm in sentence 3 commands, and only after we have completely processed this subtree does the second call become active.

Here is another way to define a throughout Chpm :

  * Change every '+' to '-' using open e-variables
  Chpm {
     e.1 '+' e.2 = <Chpm-d e.1> '-' <Chpm e.2>;
     e.1 = <Chpm-d e.1>;  }
   
  * Go down with Chpm
  Chpm-d {
     e.1 (e.2) e.3 = e.1 (<Chpm e.2>) <Chpm-d e.3>;
     e.1 = e.1;  }

When a long expression is simply printed line after line, it may be hard to read. We want to write a procedure (a ``pretty print'') which would print an expression in a more readable form. Specifically, we want all parentheses to be printed on separate lines with an offset which is proportional to the structure level of the term. Therefore, a right parenthesis should be printed in the same column as the conjugated left parenthesis.

The following program solves the problem. The idea is to keep a string of blanks as an offset and lengthen it when entering parentheses.

  * Pretty print-out of expressions
  $ENTRY Pprout { e.X = <Pprt (' ') e.X>;  }
       /* Initial offset 1 to see transfers */
   
  * <Pprt (e.Blanks-offset) e.Expression>
  Pprt {
     (e.B) e.1(e.2)e.3 = <Pr-ne (e.B) e.1>
                     <Prout e.B'('>
                     <Pprt (e.B' ') e.2>
                     <Prout e.B')'>
                     <Pprt (e.B) e.3>;
     (e.B) e.1 = <Pr-ne (e.B) e.1>;  }
   
  * Print if non-empty
  Pr-ne {
     (e.B) = ;
     (e.B) e.1 = <Prout e.B e.1>;  }

If the following expression is given to Pprout :

  '000'('111111')'00000'(('222')'111111')'0000'

  000
  (
   111111
  )
  00000
  (
   (
    222
   )
   111111
  )
  0000

  000
  (111111
  )
  00000
  ((222
   )
   111111
  )
  0000

The function Chpm defined above can be applied independently to different branches of a tree. Such functions are especially easy to define recursively. However, we often process trees in such a manner that information is passed from one branch to another. For instance, we could wish to go around a tree in a depth-first search and retain only those leaves which appear for the first time. For this purpose we need a pointer which moves around the tree, i.e., through all the structure levels of the expression.

We have already had some experience with pointers in Refal. When we process a string, the position of a pointer can be represented by a pair of parentheses; we use

  ( 'ABCDEF' ) 'GHIJKLM' 

  'ABCDEF' ^'GHIJKLM'

If Chpm were to be applied only to strings, we could define it using a pointer instead of accumulating the result in the view field:

  * Change every '+' to '-' in a string
  Chpm { e.1 = <Chpm1 ()e.1>; }
       /* set pointer at the beginning */
   
  Chpm1 {
    (e.1) '+'e.2 = <Chpm1 (e.1'-') e.2>;      
       /* move pointer and replace +*/
    (e.1) s.X e.2 = <Chpm1 (e.1 s.X) e.2>;
       /* move pointer */
    (e.1) = e.1;
       /* end of work */
        }

In this form our definition can be modified to accommodate the use of both parts of the string in the transformation. Suppose, e.g., that we do not simply replace '+' by '-' , but replace it by the full preceding string, thus doubling it (a stupid thing to do, but good enough as an illustration). Then the first sentence of Chpm1 must be rewritten as follows:

  (e1) '+'e.2 = <Chpm1 (e.1 e.1) e.2>;      

But what to do if we deal with expressions and want a pointer inside parentheses? Consider, e.g., this marked expression, i.e., an expression with a pointer:

  'AB'('C'('DEF' ^'GH')'KLM'('V')'XY') 

In a left multibracket, some number n of unpaired parentheses divides an expression into n + 1 segments. In the right multibracket there is exactly the same number n of segments separated by right parentheses. To represent a multibracket by an expression, each segment is enclosed in a pair of parentheses. For a left multibracket:

  1(2(...(n ==>(1)(2)(...)(n)

  1)2)...)n ==>(1)(2)(...)(n)

  ('AB')('C')('DEF') ^('GH')('KLM'('V')'XY')() 

Now we can replace the pointer by one more pair of parentheses, and this will be our final representation of marked expressions:

  01    11   11     1 0 1    11     2   2    111
  (('AB')('C')('DEF') ) ('GH')('KLM'('V')'XY')()

We marked the pair of parentheses representing the pointer as level 0; all other parentheses are marked starting from 1 and ignoring the pointer parentheses. Those parentheses having level 1 are multibracket format parentheses; all others are unaltered parentheses of the original expressions. To read the multibracket representation as the original marked expression, do this:

           01                  1                         
  1.Ignore (( on the left, and ) on the right end.
   
         101                                          
  2.Read ))(  as the pointer.
                                      
         11                                             
  3.Read )(  to the left/right of the pointer 
  as an unpaired left/right parentheses 
  in the left/right multibracket.

Now we have only to make the last step to use multibracket format conveniently. We accept e.ML and e.MR as standard variables for the enclosing left and right multibrackets, and introduce this notation:

  [  stands for (e.ML (
  ]  stands for )e.MR
  [. stands for ((
  .] stands for )
  ^  stands for ))(

With this notation we represent marked multibracketed expressions in the most natural way. The marked expression above becomes:

  [.'AB'('C'('DEF' ^'GH')'KLM'('V')'XY').]

Undotted square brackets are used when we write sentences in the multibracket format. The sentence by which function F moves the pointer one symbol to the right is:

  [ e.1 ^ s.X e.2 ] = <F [ e.1 s.X ^ e.2 ]>;

  [ e.1 ^ (e.2)e.3 ] = <F [ e.1 ( ^ e.2)e.3 ]>;

        [   e.1  ^ (e.2)e.3   ]  =  
     (e.ML( e.1 ))( (e.2)e.3 )e.MR = 
 
                  [   e.1 (   ^ e.2 )  e.3   ]
               (e.ML( e.1 )( ))( e.2 )( e.3 )e.MR

  e.1 = <F [. ^ e.1 .]>;

The following rule is worth remembering: when e.ML and e.MR constitute an expression, the number of terms in both of them must be the same. However, in the process of forming a new expression (as in the case of the function Pair below) e.ML and e.MR may not be so related.

We do not implement this notation as an extension of the basic Refal. It is used as a macro-notation. The programs using it must be translated, by hand or by a program, into the regular Refal so that when the programmer actually uses a Refal program he can see the translated sentences as they will actually be used by the Refal machine. The reason for this approach lies mostly in considerations of debugging. Also, in some cases we may wish to work directly with the representations of multibrackets.

The throughout function Chpm can be defined using the multibracket technique as follows:

  Chpm { e.1 = <Chpm1 [. ^ e.1 .]>; }
        /* change to MB format;
           set pointer at the beginning */
  Chpm1 {
     [ e.1 ^ '+' e.2 ] = <Chpm1 [ e.1'-' ^ e.2 ]>;
     [ e.1 ^ s.X e.2 ] = <Chpm1 [ e.1 s.X ^ e.2 ]>;
     [ e.1 ^ (e.2)e.3 ] = <Chpm1 [ e.1( ^ e.2)e.3 ]>;
     [ e.1(e.2 ^ )e.3 ] = <Chpm1 [ e.1(e.2) ^ e.3 ]>;
     [. e.1 ^ .] = e.1;  }

  refgo mbprep  source-file out-file

Sentences using multibracket macro-notation are much more readable than the actual sentences they stand for. It is a good practice to write such sentences in macro-notation and preserve them in the final program as comments. Simply make a copy of every such sentence and add an asterisk at the beginning of each line. Then call Mbprep .

Let us show the result using the function Pair as an example. The basic reading functions of Refal-5 create Refal expressions consisting of character-symbols only. If we want to convert characters '(' and ')' in such expressions into ``real'' Refal parentheses, we can use a function defined as follows:

  *** Function Pair pairs symbol-parentheses
  $ENTRY Pair{
  *  e.X = <Pair1 [. ^ e.X .]>
     e.X = <Pair1 (( ))( e.X )> };
   
  Pair1 {
  *  [ e.1 ^ '('e.2 ] = <Pair1 [ e.1( ^ e.2 ]>;
     (e.ML( e.1 ))( '('e.2 )e.MR = 
                 <Pair1 (e.ML( e.1)( ))( e.2 )e.MR>;
  *  [ e.1(e.2 ^ ')'e.3 ] = 
  *          <Pair1 [ e.1(e.2) ^ e.3 ]>;
     (e.ML( e.1)(e.2 ))( ')'e.3 )e.MR = 
             <Pair1 (e.ML( e.1(e.2) ))( e.3 )e.MR>;
  *  [. e.1 ^ ')'e.3 ] = error message;
     (( e.1 ))( ')'e.3 )e.MR = 
       <Prout "*** ERROR: Unpaired \')\' found:">
       <Prout '*** 'e.1')'>;
  *  [ e.1 ^ s.2 e.3 ] = <Pair1 [ e.1 s.2 ^ e.3 ]>;
     (e.ML( e.1 ))( s.2 e.3 )e.MR = 
             <Pair1 (e.ML( e.1 s.2 ))( e.3 )e.MR>;
  *  [. e.1 ^ .]  = e.1;
     (( e.1 ))( ) = e.1;
  *  [ e.1 ^ .] = error message;
     (e.ML( e.1 ))( ) = 
       <Prout "*** ERROR: Unbalanced \'(\' found:"> 
       <Pr-lmb e.ML>;  }
   
  *  PRint Left MultiBracket
  Pr-lmb {
     (e.1)e.2 = <Prout '*** 'e.1'('> <Pr-lmb e.2>; 
         = ;  }

When the program faces a right parenthesis which cannot be paired, the preceding expression has no multibrackets already, so we can simply print it out to indicate the location of the error. When we come to the end and there are unpaired left parentheses, the examined part of the expression is still in the multibracket format, hence we introduce Pr-lmb to print it out.

An interesting feature of the sequential multibracket format is that when we process a tree, the whole path from the pointer to the root of the tree is represented as a sequence of terms, and is thus easily accessible. We shall represent trees in the form of Refal expressions using the following rules:

• each node is represented by a symbol;
• to represent a subtree consisting of a single end-node (leaf) N we put a period after the node: N'.' ;
• to represent a non-leaf subtree that starts at N we put after N the parenthesized list of subtrees that start at the children of N: N(T₁T₂...T_n).

Thus the tree in Fig. 3.1 is written as:

  T(A(B.C.)D(E.F(G.H.I.)J.)K.) 

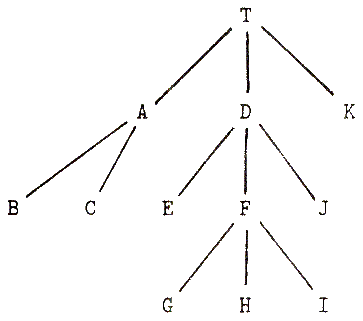
Figure 3.1 A tree of objects

  [.T(A(B.C.)D(E.F(G.H ^ .I.)J.)K.).] 

  ( (T)(A(B.C.)D)(E.F)(G.H) ) (.I.)(J.)(K.)()

Here we can trace the paths from the current point in all four directions: forwards, backwards, up, or down. If we retrace the path from the pointer (the 0 level parentheses) backwards, we see that the last object passed was H ; we can also see on the preceding branch the leaf G. , a sibling of H . To move up in the tree we move one multibracket term to the left and see that the parent of H is F . One level up we see D as a further ancestor, and then T . In the Refal expression all these objects are in the same position: the last object inside the first-level terms. Other objects, such as A , are off the path. Their form is preserved: multibracketing leaves them aside.

Because of this property of the multibracket format we can work with the path from the root of the tree to the current point using open variables. Suppose, e.g., that with trees as above we want a function to decide if a given object s.X is found in the path to the observed node. Let the function's format be:

  <In-path s.X e.Tree> 

  In-path {
     s.X (e.1(e.Sibl s.X)e.2) e.3 = True;
     e.Z = False; }