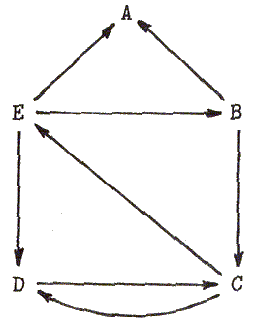
Figure 5.1 A directed graph
A directed graph is simple if there is no more than one edge with a given start and end vertices. We define a path in such a graph as a sequence of vertices where each next vertex can be reached by an edge from the preceding one. A path is acyclic if no vertex in it is repeated. We want a function which, given a graph G and a vertex V in it, will list all acyclic paths in G starting from V.
The first decision to make, as always, is the representation of the objects. We shall represent a graph in the format
s.Vertex(e.List-of-next) ...where e.List-of-next includes all those vertices which can be reached from s.Vertex by an edge (it may be empty). For instance, the graph in Fig. 5.1 is represented as:
A()B(A C)C(D E)D(C)E(A B D)

Figure 5.1 A directed graph
The shortest solution of the problem is:
Paths {
e.P(e.1 s.V e.2)(e.3 s.V(e.Next)e.4) =
<Paths e.P s.V (e.Next)(e.3 e.4)>
<Paths e.P (e.2)(e.3 s.V(e.Next)e.4)>;
e.P(e.1)(e.2) = (e.P);
}
where the initial call should be:
<Paths (V)(G)>
With the graph in Fig. 5.1 and the initial vertex E , our function results in:
(E A)(E B A)(E B C D)(E B C)(E B) (E D C)(E D)(E)()
Let us explain how we came to this solution. As often happens, it is not an original problem but its generalization that admits a straightforward recursive definition. In our case we make two generalizations: first, instead of a single starting vertex V, we consider a list of vertices Vlist, asking for the set of paths which can start with any vertex from Vlist. Second, we allow an arbitrary prefix P of the paths we compute. Thus
<Paths P(Vlist)(G)>must yield the set of paths which all start with P, then pick any of the vertices in Vlist and travel through the graph G.
The idea of the algorithm is to remove from the graph the records for those vertices which have already appeared in the path. In this way we guarantee that there will be no repeated entries in the paths we construct. In the left side of sentence 1 we see a pattern which finds the first vertex s.V for which continuation is still possible because there is a record for it in the graph. Then the set we want will consist of two subsets for which we have written two parallel recursive calls of Paths : in the first we add s.V to eP , e.Next becomes Vlist , and the record for s.V is eliminated; in the second, we look for other vertices in Vlist with the unaltered graph G. When there are no possible continuations, we give out the path P.
From the viewpoint of efficiency, however, this algorithm is faulty, because at each recursive step of Paths one extra copy of the graph (or what remains of the graph) is made. This is corrected in the following program:
$ENTRY Go { =
<Prout 'Type in the graph'>
<Br 'graph='<Input>>
<Prout 'Initial vertices, please'>
<Prout <Paths (<Input>)>>; }
$EXTRN Input;
Paths {
e.P s.1 e.Q(s.1 e.2) = <Paths e.P s.1 e.Q(e.2)>;
e.P(s.1 e.2) = <Paths e.P s.1 (<Next s.1>)>
<Paths e.P(e.2)>;
e.P() = (e.P); }
Next {
s.V, <Dg 'graph'>: e.1 s.V(e.N) e.2 = e.N
<Br 'graph=' e.1 s.V(e.N) e.2>; }
The graph is taken from the argument of Paths
and kept buried under 'graph'
.
Each time we want a continuation for a vertex,
we use the function Next
, which copies only the pertinent
part of the graph definition. We therefore have to check
at each recursive step of Path
that the candidate vertex
does not appear in the path (sentence 1).
Exercise 5.2
You might have noticed that with both versions of Paths
the empty path is one of the elements of the resulting set.
Although this is a natural consequence of our
recursive definition, it may be deemed undesirable.
Modify the program(s) so as to eliminate
the empty path.