Глава 6. Логический анализ языка
6.1. Снова о понятиях
Начнем с фундаментальнейшего понятия логики — понятия «понятие». Выше (в главе 2) мы дали кибернетическое определение этого понятия в его аристотелевском варианте. Мы определили понятие как множество ситуаций на входе кибернетической системы. Владеть понятием — значит уметь его распознавать, т. е. уметь определить, принадлежит ли любая данная ситуация к множеству, характеризующему понятие, или не принадлежит. Это определение в равной степени относится и к сложным кибернетическим системам естественного происхождения, об устройстве которых мы имеем лишь общее представление (например, мозг животного), и к тем относительно простым системам, которые создаем мы сами с прикладными или исследовательскими целями.
В первом случае мы приходим к выводу, что система распознает некое понятие, на основе наблюдения за внешними проявлениями деятельности системы. Например, когда мы видим, что собака приходит в радостное возбуждение, заслышав голос хозяина, и совсем иначе реагирует на все остальные звуки, мы заключаем, что собака имеет понятие «голос хозяина». Это понятие вырабатывается у нее естественным путем, без каких-либо усилий со стороны экспериментатора. Чтобы выявить максимальные возможности мозга собаки, экспериментатор может ставить ее в необычайные условия и следить за ее реакцией. Много опытов такого рода было проведено И.П.Павловым и его школой. Если показать собаке фанерные круги и квадраты разного размера и цвета и после предъявления круга давать пищу, а после предъявления квадрата наказывать, то собака научится различать круг и квадрат и будет по-разному реагировать на предъявление этих фигур. Следовательно, собака способна распознавать некоторые общие (абстрактные) понятия, в данном случае — понятия круга и квадрата, отвлеченные от признаков размера и цвета. Значит, мы должны заключить, что собака владеет абстрактными понятиями «круг» и «квадрат».
Но, едва произнеся эту фразу, мы начинаем чувствовать, что такое заключение, пожалуй, было бы слишком поспешным. Утверждение, что собаке доступно понятие «голос хозяина» (имеется в виду, конечно, голос конкретного человека), можно принять без оговорок, но вот утверждение, что собаке доступно понятие квадрата, представляется в каком-то смысле верным, а в каком-то нет. Заметим это себе, чтобы вернуться к этому вопросу позже. А пока завершим экскурс в область умственных способностей собаки указанием на простейшие понятия, которые собаке заведомо недоступны. Предположим, что вы показываете собаке ящик, разделенный на две части, в каждой из которых находится несколько биллиардных шаров. Вы хотите заставить ее отличить случай, когда число шаров в обеих частях одинаково, от случая, когда число шаров различно. Можно держать пари, вы не достигнете цели. Понятие равночисленности собаке недоступно.
Кибернетические системы, обладающие способностью распознавания понятий, создаются также искусственно. В связи с кибернетизацией науки и производства их значение непрерывно возрастает. Для понимания общих принципов и конкретных механизмов работы мозга разработка искусственных распознающих устройств играет решающую роль. Эти устройства служат моделями, с помощью которых люди пытаются приподнять завесу над процессом мышления. Создание «искусственного мозга», выполняющего хотя бы частично те же функции, что и естественный мозг, дает указания о том, как подходить к исследованию деятельности естественного мозга. Интересно, что одним из первых результатов сравнения искусственных и естественных распознающих систем был вывод о чрезвычайно узкой целенаправленности, специализации естественных систем. В рамках своей специализации они достигают высокого совершенства, но зато оказываются совершенно бессильными, когда задача выходит за эти рамки. Распознавание человека по голосу — чрезвычайно трудная задача для искусственных кибернетических устройств, а мозг собаки решает ее без труда. В то же время простейшая для искусственной системы задача сравнения числа биллиардных шаров непосильна для собаки.
В главе 2 мы рассматривали распознающее кибернетическое устройство, на вход которого подавались сигналы от светочувствительных рецепторов, расположенных на экране. Ситуацию, т. е. совокупность значений всех сигналов от рецепторов, мы называли «картинкой»; с точностью до полутонов она совпадает с изображением на экране. Это устройство (распознаватель картинок) послужит нам для иллюстраций и в настоящей главе.
6.2. Свойства и отношения
Примеры понятий, которые мы до сих пор приводили, укладывались в определение понятий как множества ситуаций. Но все ли понятия, которые представляются нам интуитивно ясными и проявляются в языке, таковы? Оказывается, не все. Возьмем, например, понятие, выражаемое предлогами «внутри» или «в» (в том же смысле). Если кому-нибудь не нравится, что понятие выражается предлогом, можно выразить его словосочетанием «находится в» или «нахождение в». Это понятие применимо к устройству, на вход которого подаются «картинки». Например, на рис. 6.1 пятно A находится внутри контура B. Но можем ли мы сопоставить понятию «внутри» какое-либо определенное множество картинок? Нет, не можем. Это видно, например, из рассмотрения картинок, изображенных на рис. 6.2. На картинке a пятно A находится внутри контура В, но не внутри контура C. На картинке b пятно A находится вне контура C, а пятно B — внутри него. Относить ли эти картинки к множеству ситуаций «внутри», которое нам надо было бы построить? Любой ответ будет неудовлетворительным и произвольным, ибо сам вопрос бессмыслен. Понятие «внутри» характеризует не картинку (ситуацию) в целом, а отношение между двумя определенными объектами — деталями картинки. Пока не указаны эти объекты — определенное пятно и определенный контур, ставить вопрос «внутри или не внутри» бессмысленно.
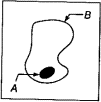
Рис. 6.1. Пятно внутри контура
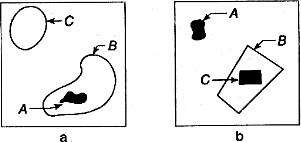
Рис. 6.2. Пятна и контура
6.3. Аристотелевская логика
Понятия, выражающие свойства ситуации в целом, мы будем называть аристотелевскими, ибо логика Аристотеля есть как раз не что иное, как последовательная теория правильного использования таких понятий. Каждому аристотелевскому понятию соответствует определенное множество ситуаций, а именно тех ситуаций, когда свойство, выражаемое этим понятием, имеет место. Поэтому аристотелевское понятие можно также описать как некое множество или класс ситуаций (явлений, объектов — в том предельно общем смысле, в котором эти термины здесь употребляются, все они равнозначны друг другу и термину «нечто», который из них самый точный, но и самый неудобный из-за необходимости считаться с грамматикой). Поэтому же все законы аристотелевской логики легко выводятся из простейших свойств операций над множествами.
Рассмотрим классический пример силлогизма.
| Все люди смертны. |
| Сократ — человек. |
|
|
| Следовательно, Сократ смертен. |
В этом рассуждении участвуют три аристотелевских понятия: «человек», «смертен» и «Сократ». Понятие «человек» характеризуется множеством ситуаций, в которых мы говорим: это — человек. То же относится и к остальным понятиям. Чтобы сделать наглядными свойства множеств, представим каждую ситуацию в виде точки внутри некоторого квадрата (рис. 6.3). Тогда этот квадрат будет олицетворять множество всех мыслимых ситуаций, что соответствует предельно общему понятию «нечто». Остальные понятия, которым соответствуют различные множества точек, будут изображаться различными областями в квадрате. Утверждение «все люди смертны», иначе говоря «каждый человек смертен», означает, что каждая точка, входящая в область «человек», входит также в область «смертен» («смертное существо»), т. е. область «человек» находится целиком в области «смертен». Точно так же вторая посылка силлогизма означает, что область «Сократ» находится целиком внутри области «человек». Отсюда следует, что область «Сократ» находится внутри области «смертен», т. е. верно утверждение «Сократ смертен».
 Нечто |
Рис. 6.3. Схема силлогизма о Сократе
 Нечто |
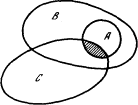
Рис. 6.4. Схема умозаключения disamis
На рис. 6.4 продемонстрирована справедливость следующей схемы умозаключения (disamis по логической терминологии).
| Все A суть B. |
| Некоторые A суть C. |
|
|
| Следовательно, некоторые B суть C. |
Логика Аристотеля играла важную роль в развитии европейской культуры. Однако она недостаточно глубоко проникает в структуру нашего мышления, она неспособна отразить процесс расчленения ситуации на отдельные части (объекты) и исследования отношений между этими частями. Когда речь идет о свойствах объектов, аристотелевская логика вполне адекватна, ибо можно представить себе изолированный объект как некую ситуацию. Образуя множество таких ситуаций-объектов, мы получаем отвлеченное понятие, выражающее одно из свойств объекта. Не так обстоит дело с отношениями. Аристотелевская логика может выразить понятие о совокупности объектов, находящихся в данном отношении, но не имеет средств выражения понятия об отношении как таковом. Можно представить множество картинок, имеющих вид контура с пятном внутри; это множество порождает аристотелевское понятие (свойство) «быть контуром с пятном внутри». Но не существует аристотелевского понятия «быть внутри». Логика Аристотеля слишком глобальна, поверхностна. Возьмем такое умозаключение:
| Иван — брат Петра. |
|
|
| Следовательно, Петр — брат Ивана. |
Умозаключение это правильно, но чтобы его обосновать, надо в явном виде добавить посылку о симметричности отношения «брат», которая здесь неявно подразумевается. Эту посылку можно выразить фразой:
Если х — брат у, то у — брат х.
Здесь буквами x и у обозначаются любые лица мужского пола. Однако такая символика выходит за пределы логики Аристотеля.
Можно ли на языке логики Аристотеля выразить этот силлогизм? Можно, если не рассматривать отдельных людей, а пары людей, точнее, упорядоченные пары, т. е. такие пары, где одному лицу приписывается номер один, а другому — номер два. Вот этот силлогизм совершенно законный с точки зрения аристотелевской логики.
| Пара (Иван, Петр) обладает свойством: первый — брат второго. |
| Каждая пара, обладающая свойством:
первый — брат второго, обладает свойством: второй — брат первого. |
|
|
| Следовательно, пара (Иван, Петр) обладает свойством: второй — брат первого. |
Это громоздкое рассуждение, хотя оно формально и совпадает с предыдущим, бъет мимо цели, ибо оно не отражает главного в нашем исходном силлогизме — симметричности отношения «брат». Свойства «первый — брат второго» и «второй — брат первого» никак не расчленены, никак не связаны друг с другом и с тем фактом, что они прилагаются к объектам, имеющим вид упорядоченной пары.
Мы не случайно начали кибернетическое исследование понятий с аристотелевских понятий. Они проще, ибо допускают определение исключительно в терминах входных и выходных состояний, без обращения к внутренней структуре распознающей системы. Так было и в истории человеческой мысли. Сначала было осознано наличие аристотелевских понятий и только гораздо позже — отношений.
Так как в математике главное — это исследование отношений между объектами, аристотелевская логика совершенно недостаточна для выражения математических доказательств. Это было замечено давно; примеры из математики, которыми пользуется традиционная логика, говорят сами за себя, они чрезвычайно примитивны и неинтересны. До самого конца XIX в., когда началось создание новой («математической») логики, математика и логика развивались независимо.
6.4. Диалектика Гегеля
В философии решающий удар аристотелевской логике нанес Гегель. Он показал своей диалектикой, что мир надо рассматривать не как совокупность объектов, обладающих некоторыми свойствами, а как совокупность объектов, находящихся в некоторых отношениях друг к другу. При этом свойства не исключаются, конечно, из рассмотрения, ибо понятие отношения является более общим, чем понятие свойства. Отношение может быть определено для произвольного числа объектов. В частности, число объектов может быть равно единице; такое отношение и есть свойство. Наиболее ясными интуитивно и в то же время наиболее важными являются парные отношения, т. е. отношения между двумя объектами. Два — минимальное число объектов при котором отношение перестает быть свойством и становится собственно отношением. Число два лежит в основе гегелевского метода что отражено в самом термине «диалектика».
Важнейшие черты диалектики Гегеля непосредственно вытекают из описания явлений в терминах отношений, а не свойств. Из такого подхода прежде всего следует учение о взаимодействии, взаимосвязанности всего сущего. Далее. Если два элемента находятся в соответствии, не противоречат друг другу, то они выступают как нечто целое и на первый план выходят их общие свойства, а взаимодействие, отношение между ними, отступает на второе место. Отношения между элементами, объектами проявляются постольку, поскольку они являются отношениями противоположности, противоречия, борьбы. Поэтому представление о борьбе противоположностей играет у Гегеля такую важную роль.
Рассматривая отношения между состоянием объекта в данный момент и состоянием этого же объекта в какой-то другой момент времени, мы приходим к понятию изменения. Изменение — это отношение между объектами, разделенными временным интервалом. На языке, оперирующем только со свойствами, но не с отношениями, изменение невыразимо. Самое большее, на что способен такой язык, это изобразить ряд никак не связанных друг с другом состояний объекта. Блестящим выражением этой неспособности является известная апория Зенона о летящей стреле. Рассмотрим летящую стрелу. Возьмем определенный момент времени. В этот момент стрела занимает определенное положение в пространстве. Возьмем другой момент времени. Стрела опять занимает вполне определенное положение в пространстве. То же относится и к любому другому моменту времени. Значит, стрела всегда занимает определенное положение в пространстве. Значит, она всегда на месте.
В аристотелевских понятиях мир представляется чем-то статическим, застывшим или, в лучшем случае, механически размноженным с некоторыми вариациями. Диалектика, напротив, сделав своим предметом исследование отношений, изучает вещи с точки зрения их изменения, движения, развития. Она вскрывает историческую обусловленность и относительность (от слова «отношения»!) вещей, которые при описании в аристотелевских понятиях представляются безусловными и вечными. Комбинация понятия противоположности с понятием отношения между состояниями в последовательные моменты времени порождает понятие об отрицании и отрицании отрицания. Диалектика динамична и революционна.
По отношению к аристотелевской логике диалектика Гегеля выступила в качестве разрушительной силы, и не только по причине своей «общей» революционности, а еще и потому, что она указала на множество противоречий, которые возникают, когда описание явлений, которое требует языка отношений, втискивается в узкие рамки языка свойств. У Гегеля и его последователей эти противоречия окружались зачастую неким ореолом возвышенности и, можно сказать, полумистической значительности. Здесь сказалось, с одной стороны, идеалистическая направленность философии Гегеля, а с другой — то общее свойство новых учений, теорий, движений, что на начальных этапах своего развития они, стараясь высвободиться из рамок старого, предпочитают парадоксальную, преувеличенную форму, приобретают героический, романтический характер. Диалектика Гегеля — это героическая эпоха новой логики, когда старый логический формализм был сломан, а новый еще не создан, и поэтому противоречивым и не поддающимся формализации («диалектическим») казалось даже то, что впоследствии оказалось прекрасно упорядоченным и формализованным. Современному мышлению, свободно пользующемуся языком отношений и вооруженному анализом логических понятий и конструкций, гегелевский стиль мышления представляется темным мудрствованием по поводу ясных вещей. Следующее рассуждение представляет собой грубо упрощенную, карикатурную схему гегелевского диалектического противоречия, показывающую, откуда это противоречие возникает.
Поставим вопрос: является ли число 1000 большим или маленьким? Оно большое, так как оно больше единицы. Оно маленькое, так как оно много меньше миллиона. Значит, оно и большое и небольшое одновременно. Диалектическое противоречие. Большое есть и в то же время небольшое, A есть не A.
Понятия «большое» и «маленькое» рассматривались здесь как свойства объектов (чисел). На самом же деле это не свойства, а замаскированные (с помощью грамматической категории прилагательного) отношения. Точный смысл можно вложить только в понятия «больше» и «меньше». Если с этой точки зрения разобрать приведенное выше рассуждение, то оно окажется просто бессмысленным. Эта карикатура направлена не против Гегеля — его заслуги в создании новой логики неоспоримы, а против тех, кто некритически относится к диалектическому методу Гегеля и во второй половине XX в. пропагандирует образ мышления первой половины XIX в., игнорируя огромный прогресс, достигнутый логикой за полтора столетия.
6.5. Математическая логика
Решающим фактором в прогрессе логики была ее математизация (конец XIX – начало XX вв.). Математизация логики была порождена потребностями математики и осуществлена математиками. Разрыв между математикой и логикой был, наконец, преодолен. Расширив свой язык и математизировав его, логика стала пригодной для описания и исследования математического доказательства. С другой стороны, для решения логических проблем стали применяться математические методы.
Завоевав плацдарм в области математики, новая логика стала проникать в естественные науки и философию. При этом роль собственно математического элемента (использование математических моделей) упала. Тем не менее всю современную логику часто называют «математической» по причине ее языка и происхождения.
6.6. Объекты и высказывания
Прежде чем продвигаться дальше в анализе языка и мышления, нам надо дать краткий набросок современной логики. Для наших целей достаточно рассмотреть только язык современной логики и те понятия, которые связаны с языком. Понятия, связанные с логическим выводом (доказательством), мы пока оставим в стороне.
Современная логика делит все сущее на объекты (или предметы) и высказывания (или утверждения). В естественном языке высказывания изображаются предложениями или наборами предложений, а объекты — словами и словосочетаниями, входящими в состав предложения. Примеры объектов: «цапля», «дядя Коля», «председатель колхоза». Примеры высказываний: «цапля сдохла», «дядю Колю выбрали председателем колхоза». Чаще всего объекты выражаются существительными, но это не обязательно. Например, «курить» — объект в высказывании «курить вредно». В приложении к математике объекты обычно называются термами, а высказывания соотношениями.
Примеры термов:
- 3.14.
- ax2 + bx + c.
- a∫bf(z)dz.
Примеры соотношений:
- aх2 + bx + c = 0.
- 0 < z < 1.
- Каково бы ни было натуральное число n > 1, найдется простое число р, которое является делителем числа n.
- Сумма квадратов катетов равна квадрату гипотенузы.
Понятия «объект» и «высказывание» считаются в логике первичными, интуитивно ясными и неопределяемыми. Формальное различие между ними состоит в том, что о высказывании имеет смысл говорить, что оно является истинным или ложным. Так, третий и четвертый примеры математических соотношений представляют собой истинные высказывания, а первое и второе соотношения могут быть истинными или ложными в зависимости от значения переменных х и z. К объектам понятия истинности и ложности неприменимы.
Объекты и высказывания, которые считаются элементарными, т. е. не расчлененными на отдельные составные части, обозначаются в логике буквами. Объекты обычно обозначаются малыми латинскими буквами, а высказывания — большими. Мы будем придерживаться этой символики, но дополнительно введем еще одно соглашение. Для ясности записи и уменьшения словесных пояснений будем иногда обозначать элементарные объекты и высказывания словами и словосочетаниями, взятыми в кавычки. Следовательно, словосочетания в кавычках будут рассматриваться на равных правах с буквами.
Объекты и высказывания, которые не являются элементарными, конструируются, очевидно, из других объектов и высказываний. Мы должны указать теперь способ конструирования.
При наличии двух типов элементов (объекты и высказывания) и предполагая, что элементы, служащие строительным материалом, принадлежат все к одному типу, мы получаем четыре возможных типа конструкций, которые мы сведем в следующую таблицу.
|
Что конструируется |
Из чего конструируется |
Название конструкции |
|
Высказывание |
Высказывания |
Логическая связка |
|
Высказывание |
Объекты |
Предикат |
|
Объект |
Высказывания |
— |
|
Объект |
Объекты |
Функция |
6.7. Логические связки
Широко употребительных логических связок пять. Это отрицание (изображается знаком ¬), конъюнкция (знак ∧), дизъюнкция (знак ∨), импликация (знак ⊃) и эквивалентность (знак ≡).
Высказывание ¬A (читается «не A») означает, что высказывание A ложно. Иначе говоря, ¬A истинно тогда, когда A ложно, и ложно тогда, когда A истинно.
Высказывание A ∧ B (читается «A и B») означает утверждение, что верно и A, и B. Оно верно только в том случае, если верны оба высказывания A и B.
Высказывание A ∨ B («A или B») верно, если верно хотя бы одно из высказываний A и B.
Высказывание A ⊃ B читается «A влечет B» или «если A, то B». Оно неверно, если A истинно, B ложно, и верно во всех остальных случаях.
Наконец, высказывание A ≡ B верно в том случае, если высказывания A и B либо оба истинны, либо оба ложны.
Для обозначения структуры связей пользуются скобками подобно тому, как это делается в алгебре для обозначения порядка выполнения арифметических действий. Так, например, высказывание ¬A ∧ B означает «A неверно, а B верно», а высказывание ¬(A ∧ B) — «неверно, что A и B оба верны». И так же, как в алгебре, для уменьшения числа скобок устанавливается порядок старшинства связок по силе связи. Выше мы перечислили связки в порядке ослабления связи. Например, конъюнкция связывает сильнее, чем импликация, поэтому высказывание A ⊃ B ∧ C понимается как A ⊃ (B ∧ C), но не как (A ⊃ B) ∧ C. Это соответствует тому, что в алгебре a + b × c означает a + (b × c), но не (a + b) × c.
Приведем несколько примеров составных высказываний.
Известная скороговорка утверждает: «цапля чахла, цапля сохла, цапля сдохла». Это высказывание можно записать в виде: «цапля чахла» ∧ «цапля сохла» ∧ «цапля сдохла».
Соотношение 0 < Z < 1 есть конъюнкция «Z > 0» ∧ «Z < 1», a соотношение |Z| > 1 — дизъюнкция «Z > 1» ∨ «Z < -1». Определение логической связки ≡ данное выше, можно записать так:
[(A ≡ B) ⊃ (A ∧ B) ∨ (¬A ∧ ¬B)] ∧ [(A ∧ B) ∨ (¬A ∧ ¬B) ⊃ (A ≡ B)]
Предоставляем читателю перевести на обычный язык следующее высказывание:
«Свет включен» ∧ «Лампочка не горит» ⊃ «Нет электричества» ∨ «Перегорели пробки» ∨ «Перегорела лампочка».
Если считать, что высказывания могут быть только истинными или ложными и, сверх этого, о высказывании ничего сказать нельзя, то перечисленных связок достаточно, чтобы выразить все мыслимые конструкции из высказываний. Достаточно даже двух связок, например отрицания и конъюнкции или отрицания и дизъюнкции. Такая ситуация имеет место, в частности, в отношении утверждений математики. Поэтому в математической логике других связок не используется.
Однако естественный язык отражает большее разнообразие в оценке высказываний, чем просто деление их на истинные и ложные. Например, высказывание можно рассматривать как бессмысленное или как недостоверное, хотя и возможное («в этом лесу, наверное, есть волки»). Этим вопросам посвящены специальные разделы логики, в которых находятся другие связки. Большого значения для современной науки эти разделы (в отличие от классической математической логики) не имеют, и мы их касаться не будем.
6.8. Предикаты
Конструкция, сопоставляющая нескольким объектам высказывание, называется предикатом. Предикаты делятся на одноместные, двухместные, трехместные и т.д. в соответствии с числом объектов, которого они требуют. Для записи их используют функциональные обозначения. Предикат можно записать в виде функции с незаполненными местами для аргументов, например
P( ), L( , ), I( , , )
или же в виде
P(x), L(z, y), I(x, y, z)
оговорив, что x, y, z — предметные переменные, т. е. символы, которые в конечном счете должны быть заменены на объекты, но какие — пока неизвестно. Впрочем, вторая форма изображает, строго говоря, уже не предикат, а высказывание, содержащее предметные переменные. Вместо больших букв мы будем также использовать словосочетания в кавычках, например,
«красный»(x), «между»(x, у, z)
и специальные математические знаки, например,
<(х, у).
Одноместный предикат выражает свойство объекта, предикат более чем с одним аргументом — отношение между объектами. Если места для аргументов в предикате заполнены, то мы имеем дело с высказыванием, утверждающим наличие данного свойства или отношения. Высказывание
«красный»(«мяч»)
означает, что «мяч» обладает свойством «красный». Конструкция
<(a, b)
равнозначна соотношению (неравенству) a < b.
Соединяя предикатные конструкции логическими связками, мы получаем более сложные высказывания. Например, соотношение |z| > 1, которое мы раньше записывали, не расчленяя высказываний на элементы, мы запишем теперь в виде
>(z, 1) ∨ <(z, -1).
6.9. Кванторы
В математике большую роль играют утверждения о всеобщности данного свойства и о существовании хотя бы одного объекта, обладающего данным свойством. Для записи этих утверждений вводятся так называемые кванторы: квантор всеобщности ∀ и квантор существования ∃. Допустим, что некоторое высказывание S содержит переменную (неопределенный объект) х, поэтому будем записывать его в виде S(x). Тогда высказывание
(∀x)S(x)
означает, что для всех х имеет место S(x), а высказывание
(∃x)S(x)
состоит в утверждении, что существует хотя бы один объект х такой, что для него верно высказывание S(x).
Переменная, входящая в высказывание под знаком квантора, называется связанной переменной, ибо высказывание от этой переменной не зависит, подобно тому как сумма
i=n∑ mSi
не зависит от индекса i. Связанную переменную можно заменить любой другой буквой, не совпадаюшей с остальными переменными, и от этого смысл высказывания не изменится. Переменная, которая не является связанной, называется свободной. Высказывание зависит только от свободных переменных, которые оно содержит.
Примеры высказываний с кванторами:
- (∀х)(∀у)(«брат»(х, у)
∧ «мужчина»(у)) ⊃ «брат»(у, x).
Для всякого х и всякого у, если х — брат у и у — мужчина, то у — брат x. - Если через D(x, y) обозначить
высказывание «x является делителем у»,
то одно из соотношений, приведенных выше
в качестве примера высказываний,
изобразится в виде
(∀n)(>(n, «1») ⊃ (∃p)D(p, n)). - (∃x)W(x) ⊃ ¬(∀x) ¬W(x).
Это соотношение верно для любого высказывания W(x) и показывает, что имеет место связь между кванторами существования и всеобщности. Из существования объекта х, для которого верно W(x), следует, что неверно утверждение, будто для всех х W(x) неверно.
Квантор — это тоже в сущности логическая связка. Приписывание квантора превращает высказывание в новое высказывание, которое содержит на одну свободную переменную меньше. Отличие от связок, которое мы рассматривали выше, состоит в том, что, кроме высказывания, надо указать еще свободную переменную, которую надо связать. Связывание переменной подразумевает подстановку вместо нее конкретных объектов. Если число объектов, которые могут быть подставлены вместо переменной, конечно, то кванторы можно рассматривать просто как удобные сокращения, ибо они могут быть выражены через логические связки — конъюнкцию и дизъюнкцию. Пусть переменная х может принимать n значений, которые мы обозначим буквами х1, х2,..., xn. Тогда имеют место следующие эквивалентности:
(∀x)W(x) ≡ W(x1) ∧ W(x2) ∧ ... ∧ W(xn),
(∃x)W(x) ≡ W(x1) ∨ W(x2) ∨ ... ∨ W(xn).
6.10. Связка «такой, что»
Третья строка таблицы, приведенной в разделе 6.6, описывает конструкцию, которая высказыванию сопоставляет объект. В естественных языках эта конструкция употребляется чрезвычайно широко. Когда мы говорим «красный мяч», мы имеем в виду объект «мяч», который обладает свойством «красный», т. е. такой, что верно высказывание «красный» («мяч»). Высказывание об объекте мы переносим в прилагательное, относящееся к существительному, которым мы обозначили объект, в других случаях для этой цели могут служить причастия, причастные обороты, обороты со связками «который», «такой, что». Если мы пойдем дальше в этом анализе, то обнаружим, что и существительное, подобно прилагательному, указывает в первую очередь на определенное свойство (свойства) объекта. Слово «мяч», как и слово «красный», изображает некоторый класс объектов и ему можно сопоставить одноместный предикат «является мячом»(х), или просто «мяч»(х). Тогда «красный мяч» это такой предмет a, что верны высказывания «мяч»(a) и «красный»(a), иначе говоря, верно высказывание
«мяч»(a) ∧ «красный»(a)
Обратите внимание: в логической записи фигурирует три независимых элемента — буква a, предметы «мяч» и «красный», а в записи на естественном языке их остается только два «красный» и «мяч». Однако буква a, которую в логическую запись вводят для того, чтобы идентифицировать данный объект, отличить его от других, и которую поэтому называют идентификатором, не совсем исчезла в естественной записи. Она перешла в понятие «мяч», превратив его из свойства в предмет! В отличие от слова «красный» слово «мяч» идентифицирует — вы можете сказать «это тот мяч, который мы потеряли вчера» или «я имею в виду тот самый мяч, о котором говорил в предыдущей фразе».
Что же такое «предмет»?
6.11. Физический предмет и логический объект
Опыт учит нас, что мир, в котором мы живем, характеризуется определенной устойчивостью, повторяемостью (точно так же, конечно, как непрерывной текучестью, изменяемостью). Допустим, вы видите дерево. Вы отходите от него, и изображение дерева на сетчатке вашего глаза изменяется. Но изменение это и его зависимость от ваших движений подчиняется определенному закону, который вам уже знаком по опыту наблюдения других предметов. А когда вы возвращаетесь на прежнее место, изображение становится почти в точности таким, как было раньше. Тогда вы говорите: «это — дерево», имея в виду не только ситуацию в данный момент времени (мгновенную фотографию), но и ситуации в близкие моменты. Если речь идет только о классификации отдельных ситуаций самих по себе без связи, без учета их отношения к другим ситуациям, то различия между предметами и свойствами никакого нет; понятие «мяч», как и понятие «красный», полностью исчерпывается указанием некоего множества ситуаций, и распознаватель этих понятий (естественный или искусственный) должен только уметь правильно употреблять фразы: «это — красное», «это — не красное», «это — мяч», «это — не мяч».
Положение меняется, когда надо классифицировать не отдельные ситуации, а временные последовательности ситуаций — будем их представлять в виде кинолент, кадры которых суть мгновенные ситуации. На такой киноленте «мяч» — это не просто деталь ситуации (одного кадра), а деталь ситуации, повторяющаяся на многих кадрах. Распознаватель понятия «мяч» должен не только сказать: «Да, друзья, это — мяч!» — но и выделить определенные детали на кадрах, сказав: «Вот этот мяч на кадре №137, а вот тот же самый мяч на кадре №138, вот он же на кадре №139 и вот он таким казался на кадре №120», — и т.д. Деталь ситуации, именуемая «тем самым мячом», может довольно существенно меняться вследствие изменения положения глаза относительно мяча или изменения формы самого мяча, но идентификация мяча как «того самого» остается неизменной и абсолютной.
Эта абсолютная неизменность является формой, в которой мы отражаем относительную и временную неизменность, которую находим в реальности. Мы как бы проводим линию во времени, соединяя детали на различных кинокадрах, и объявляем, что все, что находится на этой линии, есть «тот же самый» предмет. Эта линия в сочетании с некоторым набором свойств (качеств) и образует понятие о предмете.
Логическое понятие объекта соответствует свойству физических предметов сохранять свою идентичность. Объект логики — это только идентификатор и больше ничего. Он обладает только свойством «быть тем же самым» и является именем воображаемой линии, соединяющей детали на кадрах киноленты. Если есть несколько различных классов объектов, то обычно условливаются обозначать объекты разных классов разными типами идентификаторов, например отрезки — малыми латинскими буквами, точки — большими латинскими буквами, углы — греческими буквами и т.п. Но более конкретные свойства, присущие объектам, записываются уже в виде отдельных утверждений, включающих введение обозначения. Это позволяет обходиться без конструкции со связкой «такой, что». Правда, Бурбаки в самом начале своего знаменитого трактата «Элементы математики» вводит обозначение τx[A(x)] для некоторого объекта, обладающего свойством A(х), т. е. такого, что A{τx[A(x)]} — истинное высказывание. Однако в дальнейшем это обозначение исчезает из текста. Поэтому даже определенного названия для конструкции, сопоставляющей объект высказыванию, не установилось и в нашей таблице мы вынуждены поставить прочерк. Полное разделение труда между идентификаторами и высказываниями оказывается в конечном счете удобнее.
Возьмем для примера фразу: «Рыжий пес вдовы поручика Пшебысского загрыз бродячую кошку». При записи на языке логики эта фраза разложится на несколько высказываний, которые неявно в ней содержатся, выражаясь с помощью грамматической категории определения. Их можно объединить с помощью знака конъюнкции в одно высказывание, однако запись получится более привычной и обозримой, когда все делаемые утверждения просто выписываются, каждое с новой строчки, разделяясь запятыми вместо знаков конъюнкции. Полагая, что смысл вводимых свойств и отношений ясен из контекста, получаем следующий эквивалент указанной фразы:
«пес»(a),
«рыжий»(a),
«принадлежит»(a, b),
«вдова»(b, c),
«поручик Пшебысский»(c),
«загрыз»(a, d),
«кошка»(d),
«бродячая»(d).
6.12. Функции
В приведенном выше примере один из предикатов, а именно предикат «поручик Пшебысский»(c), отличается от остальных предикатов своей явной неэлементарностью. В свойстве «быть поручиком Пшебысским» мы различаем две стороны: иметь чин и иметь фамилию Пшебысский. Поэтому и предикат выражается двумя словами. Конечно, мы могли бы представить каждое из этих слов в виде отдельного предиката, но тот факт, что «поручик» это чин объекта c, а «Пшебысский» — его фамилия, при этом не нашел бы отражения, почему мы и сочли такое разделение бессмысленным.
«Фамилия» и «чин» — это примеры функции от одного аргумента, т. е. конструкции, сопоставляющей объекту-аргументу объект-значение функции. Функция записывается так, как это принято в математике: «фамилия»(x), «чин»(x) и т. п. Если аргументов несколько, то они отделяются друг от друга запятой и мы имеем дело с функцией нескольких переменных. Эта конструкция сопоставляет набору объектов-аргументов (порядок их важен) объект-значение. Пример функции двух аргументов: «результат игры в шахматы» (x, у). Приведем примеры функций из математики. Функции одного аргумента: sin(x), |x|. Функции двух аргументов: арифметические действия, которые можно записывать так: +(х, у), -(х, у) и т.д.; расстояние r(A, B) между двумя точками A и B в пространстве. Функции трех аргументов: угол, образуемый в точке B направлениями на точку A и C; обозначение ∠(A, B, C), сокращенно ∠ABC.
Не всякий объект можно подставить в качестве аргумента (аргументов) в заданную функцию. Если объект a — рыжий пес, то, очевидно, конструкция «чин»(a) бессмысленна. Бессмысленна и конструкция +(a, B), где a — число, а, B — точка в пространстве. Множество объектов, которые могут быть аргументами функции (для функций от многих аргументов — множество наборов объектов), называется ее областью определения. Область определения функции «чин» (x) образуют все те объекты, которые являются военнослужащими. Объекты, которые могут быть значениями данной функции, образуют множество, которое называют областью значений функции. В область значений функции «чин»(x) входят такие объекты, как «прапорщик», «поручик», «майор» и др., но никак не «3.14» или «рыжий пес». Функция «чин»(x) приписывает каждому военнослужащему определенный чин.
Когда мы имеем дело с функциями, одно из отношений между объектами становится особенно важным, а именно отношение равенства. Оно необходимо для установления соответствия между функциональными конструкциями и наименованиями объектов из области значений функций. Выделяя равенство из массы других отношений, мы сохраним для него привычную запись х = у вместо записи в виде предиката =(х, у). Тот факт, что объект c имеет фамилию «Пшебысский» и чин «поручик», будет выглядеть следующим образом:
(«фамилия»(c) = «Пшебысский») ∧ («чин»(c) = «поручик»).
Отношение равенства можно определить формально с помощью следующих четырех утверждений:
- (∀a)(a = a).
- (∀a)(∀b)[(a = b) ⊃ (b = a)].
- (∀a)(∀b)(∀c)[(a = b) ∧ (b = c) ⊃ (a = c)].
- (∀a)(∀b)[(a = b) ⊃ (W(a) ≡ W(b))].
Последнее утверждение верно для любого высказывания W(x), зависящего от переменной х. В качестве упражнений предлагаем читателю перевести эти утверждения на естественный язык.
В одном из примеров, приведенных выше, мы видели предикат D(x, y), имеющий смысл: «x является делителем у». Понятие делимости целиком определяется операцией (функцией) умножения, поэтому предикат D(x, у) может быть выражен через функцию. Натуральное (т. е. целое положительное) число p является делителем числа n тогда и только тогда, когда существует такое натуральное число т, что n = p × m. На языке исчисления предикатов
(∀p)(∀n)[D(p, n) ≡ (∃m)(n = ×(p, m))].
Каждой функции от n аргументов можно поставить в соответствие n+1-местный предикат, выражающий то отношение, что один (скажем, последний) аргумент есть данная функция от остальных аргументов. Например, функции ×(x, y) соответствует предикат M(x, y, z), который дает верное высказывание в том и только в том случае, когда z = ×(x, y). В общем случае функции f(x, у, ..., z) соответствует предикат F(x, у, ..., z, u), обладающий свойством
(∀x)( ∀y)...(∀z)( ∀u)[F(x, у, ..., z, и) ≡ (f(x, у, ..., z) = u)].
Предикат F выражает фактически то же понятие, что и функция f. Любое высказывание, содержащее функциональные символы, можно переписать, используя лишь предикатные символы и введя дополнительно некоторое число объектных переменных. Таким образом, обе конструкции, порождающие новые объекты, — конструкция со связкой «такой, что» и функция — не являются принципиально необходимыми и без них можно обойтись. Однако в отличие от конструкции «такой, что» функциональные символы весьма удобны и широко используются в логике.
6.13. Синтаксис и семантика
В заключение нашего краткого очерка логики рассмотрим вопрос о связи языка логики и естественного языка. Попутно будут введены важные понятия синтаксис и семантика языка.
Вспомним фразу о рыжем псе, которую мы разложили в набор высказываний, выражаемых с помощью предикатов. Смысл, значение, этого набора совпадает со смыслом исходной фразы, а форма записи, структура текста, существенно отличается. В семиотике (наука, изучающая знаковые системы) совокупность правил построения элементов языка называют его синтаксисом, а связь между элементами языка и их значениями — семантикой. Следовательно, первое, что бросается в глаза при сравнении логического и естественного языков, это то, что язык логики имеет другой синтаксис. Этот синтаксис прост и единообразен. Он основан на стиле обозначений, сложившемся в математике, — конструирование более сложных элементов языка из более простых, изображается по аналогии с математической записью операций и функций. Синтаксис языка логики полностью формализован, т. е. существует набор четко сформулированных правил, с помощью которых можно построить любой языковый элемент. Далее, какой бы правильно построенный элемент языка (объект или высказывание) мы ни взяли, всегда можно восстановить путь, которым этот элемент был построен, его структуру. Этот процесс называется синтаксическим анализом элемента. Легко убедиться, что в языке логики синтаксический анализ чрезвычайно прост и однозначен.
Синтаксис (в смысле семиотики) естественного языка — это его грамматика, т. е. правила конструирования предложений из слов (синтаксис в узком, лингвистическом смысле слова) и правила конструирования слов из букв (морфология). В отличие от языка логики синтаксис естественного языка отнюдь не является полностью формализованным. Он включает в себя множество правил с великим множеством исключений. Это различие вполне понятно: язык логики создавался искусственно, а естественный язык — продукт долгого развития, которым никто не управлял сознательно, никто не пользовался заранее продуманным планом. Грамматика естественного языка — это не конструирование, а исследование уже готовой системы, попытка вскрыть и по возможности сформулировать те правила, которыми говорящие на этом языке люди пользуются неосознанно.
Синтаксический анализ предложений естественного языка нередко требует обращения к семантике, ибо без учета смысла, значения предложения, он оказывается неоднозначным. Возьмем, например, такую фразу: «Вот списки студентов, которые сдали зачет по физике». Здесь определение «которые сдали зачет по физике» относится к студентам. Если для уточнения синтаксической структуры фразы использовать скобки подобно тому, как это делается при записи алгебраических или логических выражений, то скобки надо поставить так: «Вот списки (студентов, которые... и т. д.)». Теперь возьмем такое предложение: «Вот списки студентов, которые лежали в шкафу у декана». Формально структура этой фразы в точности такая же, как и предыдущей. На самом же деле здесь подразумевается другая расстановка скобок, а именно «Вот (списки студентов), которые... и т. д.». Мысленно расставляя скобки таким образом, мы опираемся исключительно на смысл фразы, ибо не допускаем, что студенты могли лежать в шкафу у декана.
Вообще оборот со словом «который» — весьма коварная вещь. Л.Успенский в книге «Слово о словах» рассказывает, что однажды он увидел такое объявление:
«Граждане, сдавайте утиль дворнику, который накопился!»
Неудивительно, что этот оборот не прижился в математической логике!
6.14. Логический анализ языка
Итак, для логического анализа, т. е. для построения логического эквивалента фразы естественного языка, мы должны прежде всего провести синтаксический анализ фразы; результаты анализа непосредственным образом отразятся на синтаксической структуре логического выражения. Но и семантика отнюдь не останется в стороне. Когда мы говорим, что «рыжий» — это одноместный предикат, «загрыз» — двуместный предикат, «расстояние» — функция, «и» — логическая связка, «все» — квантор и т.д., мы выполняем семантический анализ понятий, выражаемых естественным языком. Мы классифицируем понятия в соответствии со схемой, зафиксированной в языке логики, и устанавливаем связь между понятиями. Логический анализ — это по существу семантический анализ. Синтаксический анализ нужен постольку, поскольку он необходим для семантического.
Логический анализ может быть более или менее глубоким. В нашем примере он весьма поверхностен. Посмотрим, могли бы мы его продолжить, и если да, то как именно.
Понятия «пес», «рыжий» и «кошка» — одноместные предикаты, которые можно признать элементарными и не подлежащими дальнейшему анализу. Это простые аристотелевские понятия, опирающиеся непосредственно на чувственный опыт; каждый нормальный человек умеет их распознавать, и единственный способ объяснить, что такое «кошка», — это показать кошку.
Понятие «бродячая» — тоже одноместный предикат, но уже более сложный. Рассуждая формально грамматически, можно было бы заключить, что «бродячая» означает «которая бродит». Но это было бы неверным заключением, ибо глагол «бродит» не указывает длительности время провождения, которое он именует. Вполне добропорядочная семейная кошка может выйти на часок побродить по крыше, и это никому не дает права назвать ее «бродячей». Правильнее определить бродячую кошку как кошку, у которой нет хозяина, или же, пользуясь отношением, которое уже входит в наше логическое выражение, как кошку, которая никому не принадлежит. Вот формальная запись этого определения:
«бродячий»(x) ≡ ¬(∃y)(«принадлежит»(x, y)).
(Здесь подразумевается, что х — произвольный объект.)
Обратимся к отношению «принадлежит». Мы ввели его, в некотором смысле, контрабандой, ибо слова «принадлежать» не было в исходной фразе. Но оно подразумевалось и семантический анализ выявил его! Отношение принадлежности передавалось в русской фразе родительным падежом. Здесь мы видим яркий пример неоднозначности и недостаточности синтаксического анализа. Тот же самый родительный падеж, который используется в конструкции «собака вдовы», используется в конструкции «хозяйка собаки», но никак нельзя сказать, что хозяйка «принадлежит» своей собаке. Конструкцию «нос вдовы» можно, конечно, истолковать как «нос, который принадлежит вдове». Но здесь мы уже встречаемся, с семантической неоднозначностью слова «принадлежит», ибо нос, очевидно, принадлежит вдове не так, как принадлежит ей собака.
Чтобы разложить понятие «принадлежит» на элементарные составные части, надо проделать изрядную работу: описать обычаи и законы, связанные с правом собственности. Только в этом случае можно объяснить, что значит «принадлежит». Предикат «вдова» и функции «чин» и «фамилия» (которые мы уже ввели, анализируя понятие «поручик Пшебысский») также связаны с социальной сферой и требуют дальнейшего анализа. Наконец, понятие «загрыз», хотя оно и не связано с социальной сферой и явно проще (ближе к чувственному опыту), чем предыдущие понятия, также могло бы быть подвергнуто логическому анализу. В нем можно выделить, во-первых, элемент завершенности действия, выражающийся глагольной формой, во-вторых, конечный результат — смерть жертвы и, в-третьих, характерную особенность действия — использование зубов.
Логический анализ языка — чрезвычайно интересное направление исследований, но мы не можем останавливаться на нем более фундаментально. Интересующихся отошлем к книге одного из основоположников этого направления Г.Райхенбаха1.
Итог сравнения естественного языка и языка логики подведем следующим образом. Язык логики обладает простым и полностью формализованным синтаксисом. Текст на естественном языке можно путем синтаксического и семантического анализа перевести на язык логики, т. е. сопоставить ему текст на языке логики, имеющий тот же смысл. Семантический анализ естественного текста при переводе может быть более или менее глубоким, т. е. предикаты и функции, входящие в логический текст, могут быть ближе или дальше от непосредственного чувственного и духовного опыта. Существуют такие предикаты и функции, которые разложимы на более элементарные слагающие и которые поэтому нельзя определить иначе, как сославшись на опыт. Такие предикаты и функции мы будем называть первичными.
1 Reihenbuch H. Elements of symbolic logic. New York, 1960.